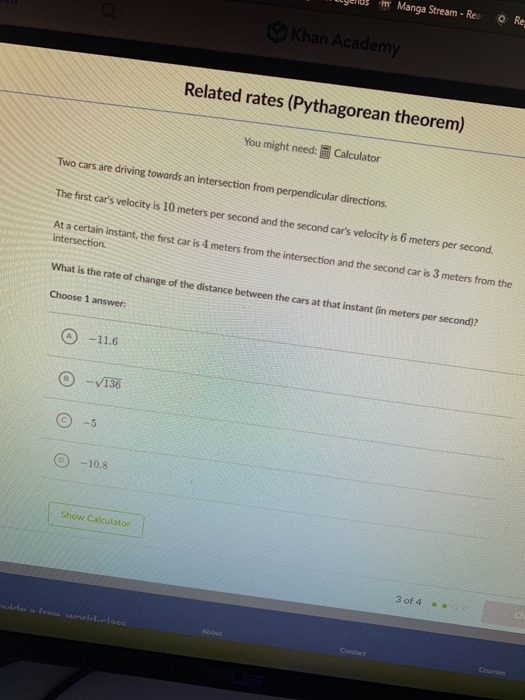
Khan Academy Related Rates

Khan Academy Related Rates - Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the. If you're seeing this message, it means we're having trouble loading external resources on our website. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍ millimeters. Given a related rates problem, pick the appropriate equation to relate the relevant quantities. If you're behind a web filter, please. The related rates exercise appears under the differential calculus math mission and integral calculus math mission.

The related rates exercise appears under the differential calculus math mission and integral calculus math mission. Given a related rates problem, pick the appropriate equation to relate the relevant quantities. Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍ millimeters. If you're seeing this message, it means we're having trouble loading external resources on our website. If you're behind a web filter, please.

Given a related rates problem, pick the appropriate equation to relate the relevant quantities. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍ millimeters. The related rates exercise appears under the differential calculus math mission and integral calculus math mission. If you're seeing this message, it means we're having trouble loading external resources on our website. If you're behind a web filter, please. Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the.

Rate conversion Khan Academy YouTube

The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍ millimeters. The related rates exercise appears under the differential calculus math mission and integral calculus math mission. Given a related rates problem, pick the appropriate equation to relate the relevant.

o9 Solutions corporate yearend grant donation to Khan academy o9

If you're seeing this message, it means we're having trouble loading external resources on our website. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍ millimeters. Using our knowledge of angles, distances, and related rates we can apply trigonometry.

Khan Academy MathsConnect India

If you're seeing this message, it means we're having trouble loading external resources on our website. Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the.

82 Khan Academy Statistics for 2024 (Data & Facts)

Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the. The related rates exercise appears under the differential calculus math mission and integral calculus math mission. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the.

Related rates shadow Applications of derivatives AP Calculus AB

If you're seeing this message, it means we're having trouble loading external resources on our website. Given a related rates problem, pick the appropriate equation to relate the relevant quantities. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍.

Khan Academy Net Worth & Earnings (2024)

If you're seeing this message, it means we're having trouble loading external resources on our website. If you're behind a web filter, please. Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the. The base of a triangle is decreasing at a rate of 13 ‍ millimeters.

Related rates Falling ladder Applications of derivatives AP

The related rates exercise appears under the differential calculus math mission and integral calculus math mission. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍ millimeters. If you're seeing this message, it means we're having trouble loading external resources.

Related rates Approaching cars Applications of derivatives AP

Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is increasing at a rate of 6 ‍ millimeters. If you're seeing this message, it.

Solved gelu Manga StreamRea Re Khan Academy Related rates

Given a related rates problem, pick the appropriate equation to relate the relevant quantities. If you're seeing this message, it means we're having trouble loading external resources on our website. If you're behind a web filter, please. The base of a triangle is decreasing at a rate of 13 ‍ millimeters per minute and the height of the triangle is.

Khan Academy Donate Comparing rates Coach Salinas wants to compare the

If you're behind a web filter, please. If you're seeing this message, it means we're having trouble loading external resources on our website. Using our knowledge of angles, distances, and related rates we can apply trigonometry and calculus to find the rate of change in the. The base of a triangle is decreasing at a rate of 13 ‍ millimeters.